- Estampillage UOH (44)
- Arts (8)
- Arts visuels et plastiques (8)
- Arts graphiques, gravures et estampes (7)
- Dessin et arts décoratifs (1)
- Arts-Approches transversales et méthodologie (1)
- Approches transversales (1)
- Arts visuels et plastiques (8)
- Langues, Littératures et Civilisations étrangères (2)
- FLE - Français langue étrangère (2)
- FLE - Français langue étrangère (2)
- FLE - Français langue étrangère (2)
- Lettres classiques, Langues et Littératures françaises et de France (8)
- Langue française (8)
- Français (7)
- Langage (1)
- Littératures française et de langue française (1)
- Poésie (1)
- Langue française (8)
- Sciences de l'homme (38)
- Homme-Approches transversales et méthodologie (11)
- Méthodologie (11)
- Philosophie (20)
- Les divers systèmes et écoles philosophiques modernes (1)
- Logique (1)
- Philosophie politique (5)
- Épistémologie, causalité, genre humain (14)
- Psychologie (1)
- Psychologie appliquée et comparée (1)
- Sciences des religions (5)
- Histoire et théorie de la religion - concepts transversaux - analyses comparées (5)
- Sciences du langage (6)
- Sociolinguistique (6)
- Homme-Approches transversales et méthodologie (11)
- Sciences de la société (58)
- Histoire, Histoire de l'Art, Archéologie (10)
- Histoire générale (10)
- Sciences de l'information et de la communication (17)
- Bibliothéconomie - Sciences de l'information (2)
- Le livre (7)
- Médias documentaires et éducatifs - Journalisme - Édition (2)
- Théorie de la communication (3)
- Télécommunications (4)
- Sciences de l'éducation (4)
- TICe (4)
- Sociologie, Démographie, Anthropologie (16)
- Sociologie des processus sociaux (16)
- Société-Approches transversales et méthodologie (17)
- Approches transversales (17)
- Statistiques, Informatique et Mathématiques appliquées aux sciences humaines et sociales (33)
- Informatique - Traitement et programmation des données (14)
- Mathématiques appliquées aux sciences sociales (1)
- Méthodes informatiques particulières (3)
- Statistiques appliquées aux sciences sociales (15)
- Histoire, Histoire de l'Art, Archéologie (10)
- Enseignement supérieur (81)
- L1 (35)
- L2 (12)
- L3 (20)
- Licence (77)
- M1 (23)
- M2 (18)
- Master (26)
- bac>=6 (1)
- Autoévaluation (12)
- Autres (1)
- Conférence, table ronde et entretien (type UOH) (8)
- Essentiel (type UOH) (43)
- Etude de cas (2)
- Etude et document (type UOH) (4)
- Exercice (7)
- Grande Leçon (type UOH) (33)
- Guide pédagogique (4)
- Jeu sérieux (1)
- Webographie, bibliographie (9)

Mathématiques et réalité (Cours : Six questions cl...
Dans l’animation : « Les escargots font-ils des maths ? » on peut rencontrer Einstein, Galilée, Copernic mais aussi un escargot, une marguerite et un nain de jardin ! Elle pose la question de l'énigmatique correspondance entre les mathématiques et la nature.
Un débat entre un mathématicien et un philosophe, Philippe Lombard Maître de Conférences à l'Université de Lorraine, Membre de l'Institut Elie Cartan – Nancy, responsable du petit séminaire IREM, Groupe "M", Archives Poincaré et Thomas Benatouïl Maître de Conférences en Philosophie à l'Université de Lorraine, Membre junior de France, Membre des Archives Henri Poincaré nous raconte comment s’est déroulé à travers les époques le dialogue entre mathématiques et physique.
Le débat s’articule sur les 4 thèmes suivants :
- mathématiques et réalité dans l'antiquité grecque : l’époque où le cercle régnait en maitre dans le ciel.
- la « déraisonnable efficacité des mathématiques » : pourquoi les mathématiques s’appliquent-elles si bien à la nature ?
- la cristallographie et l'histoire d'un prix Nobel : un exemple du dialogue entre mathématiques et physique au xxème siècle
- les allers retours entre mathématiques et physique : où l’on voit que l’influence entre mathématique et physique est réciproque

À propos des mathématiques financières
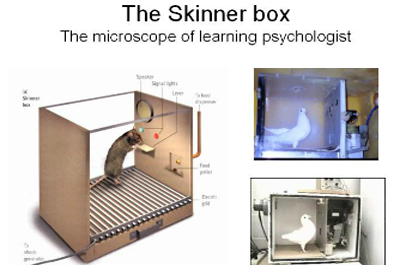
Temporal learning in animals - L'apprentissage tem...
Empirical tests of two mathematical models of timing. Armando Machado : University of Minho, Portugal.

Espoir et théorie des catastrophes. L'intelligibil...
Fondée dans les années 70 par le mathématicien René Thom, la théorie des catastrophes devient rapidement, malgré l'engouement qu'elle suscite, sujet de controverse et de critique. Visant à décrire les phénomènes discontinus à l'aide de modèles mathématiques continus, elle se définit comme un langage mathématique, un outil d'intelligibilité du monde mais son manque de rigueur et sa nature qualitative laissent sceptiques positivistes et mathématiciens purs. Bien que ces critiques n'aient que partiellement entamé son expansion puisque ses domaines d'application s'étendent au fil du temps de la biologie aux disciplines de sciences humaines telles que l'éthologie et la psychologie (théorie de Harry Blum), elles sont à l'origine du désintérêt des chercheurs pour ce langage mathématique apte selon Luc Gootjes à relever de nouveaux défis scientifiques.

Entretien avec Epaminondas Vamboulis - Recherche ...
La physique et la philosophie naturelle de Spinoza. Cet entretien traite du mouvement, de la matière et plus généralement de la nature chez Spinoza. Épaminondas Vamboulis s'intéresse à la question de l'appropriation par Spinoza de la physique cartésienne, et plus généralement à l'histoire des sciences et à la philosophie naturelle au 18ème siècle. Il évoque notamment Les Principes de la philosophie de Descartes, texte où Spinoza reprend les thèses de Descartes et propose des solutions inédites. Pour finir, il évoque son champ d'étude actuel : le rapport de la pensée de Spinoza avec les sciences de son temps en général, et notamment avec les mathématiques. Entretien par Pierre-François Moreau

Mathématiques : les suites numériques (Filière Lin...

Mathématiques : notions de base (Filière Linguisti...

La logique est-elle barbante ? (La philo en petits...
Ce sixième épisode met en scène le paradoxe de Russel, communément appelé le paradoxe du barbier, ainsi que sa résolution par les logiciens au début du 20ème siècle. Le lien entre la logique et les mathématiques, ainsi que l'enjeu de fondation liant la première aux secondes, sont ainsi abordés.
Ludique et pédagogique, ce court film d'animation sur la philosophie des sciences émane de la série La Philo En Petits Morceaux.

Introduction à la logique (Cours : Six questions c...
La logique est- elle barbante ? : En s’appuyant essentiellement sur le paradoxe de Russel, communément appelé le « paradoxe du barbier », l’animation introduit un problème de logique qui a interrogé les plus grands mathématiciens et logiciens au début du 20 ème siècle.
Amirouche Moktefi Chercheur associé à l'IRIST (Strasbourg) et au LHSP - Archives H. Poincaré (Nancy) présente les notions de base de la logique, à partir d’un paradoxe introduit par Lewis Caroll (écrivain et logicien) dans « Alice au pays des merveilles ».
Problème flash dans l'introduction.







